Método Horner División Polinomios - Ejercicios Resueltos
Para dividir dos polinomios por el método de Horner, primeramente se trazan dos rectas que se intersecten, una vertical y otra horizontal. Encima de la recta horizontal y la derecha de la vertical se colocan los coeficientes del dividendo con su propio signo. A la izquierda de la recta vertical se coloca el primer coeficiente del divisor con su propio signo y debajo de la horizontal se colocan el resto de coeficientes del divisor con signo cambiado.
En el vídeo que se muestra a continuación se explica el método con varios ejemplos resueltos.
Solamente se puede aplicar la Regla de Ruffini cuando el divisor es un binomio de la forma: (x - a). Por ejemplo: (x - 3), (x + 2), (x - 1/2), etc.
Para aplicar la Regla de Ruffini, se ponen los coeficientes de dividendo-completo y ordenado de mayor a menor grado-, y el opuesto del número "a" del divisor (El opuesto del término independiente. Si es una suma, queda un número negativo. Si es una resta, queda un número positivo). Las x (o letras) del polinomio se quitan, y se hacen determinadas operaciones entre los números (ver en la EXPLICACIÓN todos los pasos). Luego, en el resultado, el último número de la derecha es el Resto de la división; y los otros números son los coeficientes del Cociente (resultado de la división), a los que hay que agregarles las "x" en orden de izquierda a derecha, comenzando por un grado menos que el del dividendo y disminuyendo hasta llegar a un término independiente (grado cero).
Para aplicar la Regla de Ruffini, se ponen los coeficientes de dividendo-completo y ordenado de mayor a menor grado-, y el opuesto del número "a" del divisor (El opuesto del término independiente. Si es una suma, queda un número negativo. Si es una resta, queda un número positivo). Las x (o letras) del polinomio se quitan, y se hacen determinadas operaciones entre los números (ver en la EXPLICACIÓN todos los pasos). Luego, en el resultado, el último número de la derecha es el Resto de la división; y los otros números son los coeficientes del Cociente (resultado de la división), a los que hay que agregarles las "x" en orden de izquierda a derecha, comenzando por un grado menos que el del dividendo y disminuyendo hasta llegar a un término independiente (grado cero).
EJEMPLO 2: (El dividendo A no tiene término independiente)
A = -4x4 + 30x + x5
B = x - 3
A : B = (-4x4 + x5 + 30x) :(x - 3)
1) Polinomio A ordenado y completo: x5 - 4x4 + 0x3 + 0x2 + 30x + 0
2) El opuesto del término independiente del polinomio divisor: 3
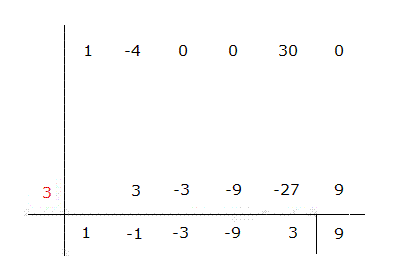
Cociente = x4 - x3 - 3x2 - 9x + 3
Resto: 9
A = -4x4 + 30x + x5
B = x - 3
A : B = (-4x4 + x5 + 30x) :(x - 3)
1) Polinomio A ordenado y completo: x5 - 4x4 + 0x3 + 0x2 + 30x + 0
2) El opuesto del término independiente del polinomio divisor: 3
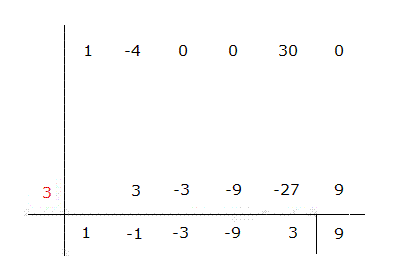
Cociente = x4 - x3 - 3x2 - 9x + 3
Resto: 9
No hay comentarios:
Publicar un comentario